OA1=x·OA |
|
Скачать презентацию |
||
| << Признак компланарности трех векторов | Правило параллелепипеда >> |
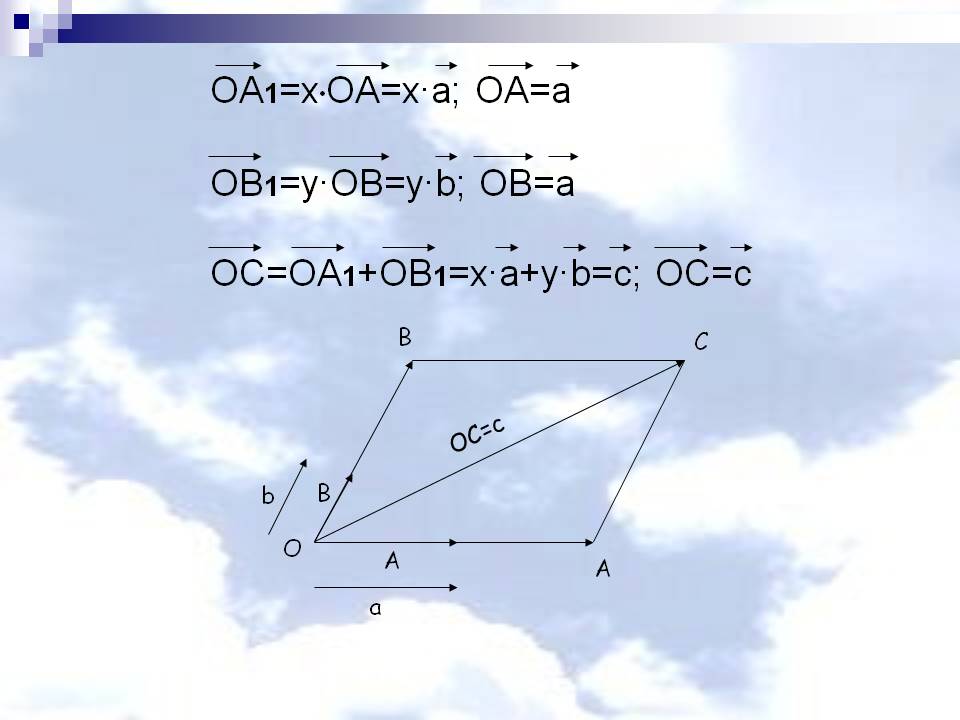
OA1=x·OA=x·a; OA=a OB1=y·OB=y·b; OB=a OC=OA1+OB1=x·a+y·b=c; OC=c. B. C. OC=c. B. b. O. A. A. a.
Скачать презентацию
Геометрия 11 класс
краткое содержание других презентаций«Философ Пифагор» - Египетские храмы. Математика. Бессмертная идея. Основоположник современной математики. Знание основ музыки. Мнесарх. Пифагор. Мысль. Истина. Направление полёта. Девиз. Пифагор встречался с персидскими магами. Слово "философ". Жизнь и научные открытия Пифагора.
«Объёмы геометрических тел» - Объем пирамиды. Объем прямой призмы. Свойства площадей. Квадрат. Ответ. Объемы тел. Объем цилиндра. Объемы многогранников. Понятие объема. Геометрия. Найдите объем цилиндра. Площадь. Понятие объема тел. Рисунки и чертежи. Конус выноса. Три латунных куба. Объем правильной четырехугольной пирамиды. Ребро куба. Науки стремятся к математике. Геометрические фигуры. Объем прямоугольного параллелепипеда.
«Понятие центральной симметрии» - Задача. Движение пространства. Отображение пространства на себя. Точки М и М1 называются симметричными. Центральная симметрия является движением. Движения. Центральная симметрия является частным случаем поворота. Мы знакомились с движениями плоскости. Фигура называется симметричной. Центральная симметрия. Свойство.
«Понятие цилиндра» - Цилиндры в архитектуре. Кружки. Задачи на тему «Цилиндр». Ножницы. Тело вращения. Счастье было потеряно навсегда. Прямоугольник. Объем цилиндра. Добрые ножницы. Два милых кружочка. Школьник. Откуда и как появился цилиндр. Не правда ли захватывает дух. Площадь поверхности цилиндра. Чудо. Цилиндры вокруг нас. Сечения цилиндра. Вписанный и описанный цилиндр. Цилиндр. Как появился цилиндр. Тетрадь. Кружочки.
«Площадь сферы» - Радиус сферы (R). В куб с ребром 3 вписан шар. Тогда объем шара. Vш. сектора= 2/3ПR2h. Основание сегмента. Площадь большого круга шара равна 3. Найдите площадь поверхности шара. Радиус вписанного в куб шара равен половине длины ребра: Радиус шара (R). Из условия. Найдем, что радиус такого шара. При увеличении радиуса втрое, объем шара увеличится в 27 раз. , то есть в 1,5 раза меньше первой. Sсферы= 4ПR2.
««Задачи по геометрии» 11 класс» - Диаграмма отражает сравнение результатов самостоятельной работы. Технология проекта. Около треугольной призмы описана сфера, центр которой лежит вне призмы. Использование компьютера на уроках. В правильную треугольную пирамиду вписан шар. В правильную четырехугольную усеченную пирамиду можно вписать сферу. Найти радиус описанной сферы. Найдите боковое ребро призмы. Сфера, вписанная в правильную треугольную призму.
Всего в теме «Геометрия 11 класс» 45 презентаций