Назовите пары параллельных прямых |
|
Скачать презентацию |
||
| << Продолжите предложение: Два треугольника равны, если … | Определение Четырехугольник, у которого противоположные стороны >> |
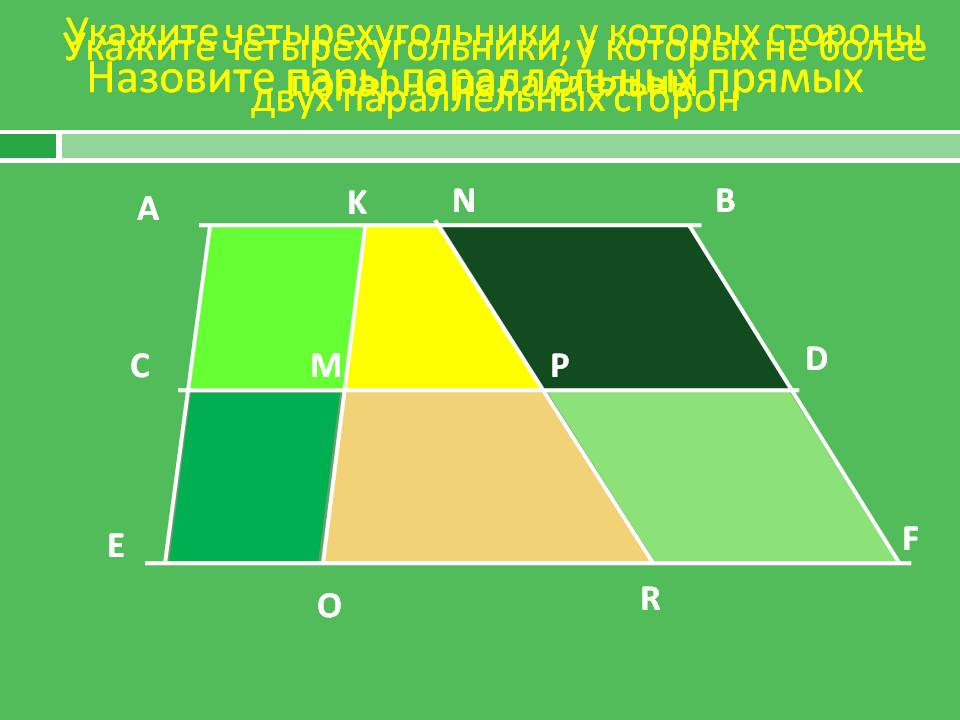
Назовите пары параллельных прямых. Укажите четырехугольники, у которых стороны попарно параллельны. Укажите четырехугольники, у которых не более двух параллельных сторон. N. B. K. А. D. C. M. P. F. E. R. O.
Скачать презентацию
Геометрия 8 класс
краткое содержание других презентаций«Геометрия Параллелограмм 8 класс» - Продолжите предложение: Два треугольника равны, если … 1. D. F. Соответственные углы равны. ? 1 + ? 2 = 180?. Назовите пары параллельных прямых. b. B. Продолжите предложение: При пересечении двух параллельных прямых третьей секущей…
«Формула Герона» - Х+у=с. В. Формула Герона. Вывод формулы Герона геометрия 8 класс. Доказательство: А. Н. Площадь треугольника со сторонами a,b,c выражается формулой где полупериметр треугольника. A b c y х h. Треугольники АCН и ВСН – прямоугольные. С.
«Ромб 8 класс» - Автор: учащийся 8 класса Шумков Ю. Ромб. Цель исследования: Задачи исследования:
«Симметрия в геометрии» - C1. Фигура может иметь несколько осей симметрии. Я в листочке, я в кристалле, Я в живописи, архитектуре, Я в геометрии, я в человеке. Симметрия относительно прямой. C. Симметрия относительно точки. А точечка О, симметрии центр, Бывает же только одна. F. Вот центр, вот ось. Задание: провести лучевую симметрию. Задание: провести оси симметрии на живых объектах. D.
«Урок Теорема Пифагора» - Исторический экскурс. a. Показ картинок. Разминка. План урока: Исторический экскурс. Урок геометрии, 8 класс. Домашнее задание. Доказательство теоремы. c. Теорема Пифагора. МОУ-СОШ с. Батурино Учитель математики Леонова Надежда Александровна. Закрепление.
«Уравнение окружности» - Повторение. Уравнение окружности. №1. Вывод формулы. (х – а)2 + (у – b)2 = R 2 . №4. А(а;b) – центр окружности, С(х ; у) – точка окружности. d 2 = АС 2 = (х – а)2 + (у – b)2, d = АС = R, следовательно R 2 = (х – а)2 + (у – b)2. №5.
Всего в теме «Геометрия 8 класс» 69 презентаций