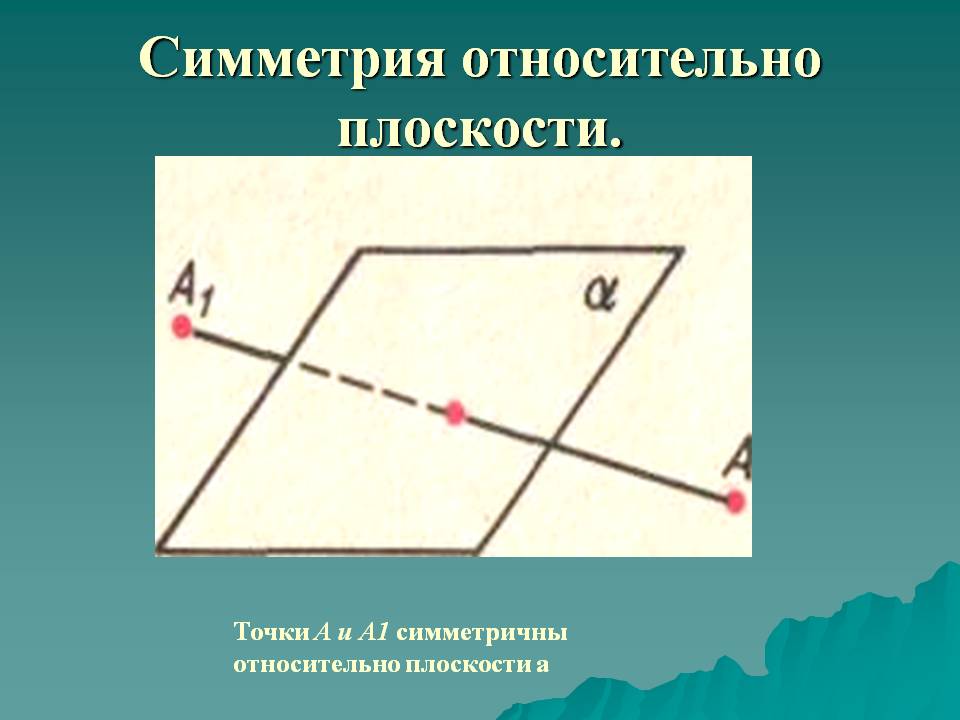
Симметрия относительно плоскости

Геометрия 8 класс

«Площади фигур» - Основные свойства площадей. Площадь. SABCDEF=SA1B1C1D1E1F1. В. D. А=1. Площадь квадрата со стороной 1 равна 1. Разрезания и складывания. Sавс = sа1в1с1. А. F1.

«Урок Площадь трапеции» - Задание. V.Проверка усвоения изученного. Сумма оснований равна… Запишите только решение. Записывают в тетради тему урока, чертят трапецию. Что общего в формулах площадей ? Оценивают свою работу в баллах. Подсчитывают количество полученных баллов в данном задании. Деятельность учащихся:

«Урок Теорема Пифагора» - a. Разминка. МОУ-СОШ с. Батурино Учитель математики Леонова Надежда Александровна. Домашнее задание. План урока: Исторический экскурс. Теорема Пифагора. Урок геометрии, 8 класс. Доказательство теоремы. Показ картинок. c. Закрепление. Исторический экскурс.

«8 класс Симметрия» - Какие прямые называются перпендикулярными? Изучение нового материала. Каково взаимное расположение прямых на плоскости? Сколько и какие оси симметрии имеет квадрат? прямоугольник? окружность? Цель урока: Какие прямые называются параллельными? Урок геометрии 8 класс Иванова Светлана Ивановна. Какие геометрические фигуры имеют ось симметрии? 0 1 2 3 4 5 6 7 8 9.

«Многоугольники 8 класс» - К. М. А. Учитель математики высшей категории Никитина С.Е. С. В. Р. Д. Е. МНОГОУГОЛЬНИКИ 8 класс (презентация к уроку).

«Уравнение окружности» - А(а;b) – центр окружности, С(х ; у) – точка окружности. d 2 = АС 2 = (х – а)2 + (у – b)2, d = АС = R, следовательно R 2 = (х – а)2 + (у – b)2. Формула I. Уравнение окружности. Центр окружности О(0;0), (х – 0)2 + (у – 0)2 = R 2, х2 + у2 = R 2 ? уравнение окружности с центром в начале координат. . О (0;0) – центр, R = 4, тогда х2 + у2 = 42; х2 + у2 = 16. Формула II. Повторение.