Область значений – множество всех положительных чисел |
|
Скачать презентацию |
||
| << Свойства показательной функции | Функция возрастает на всей области определения >> |
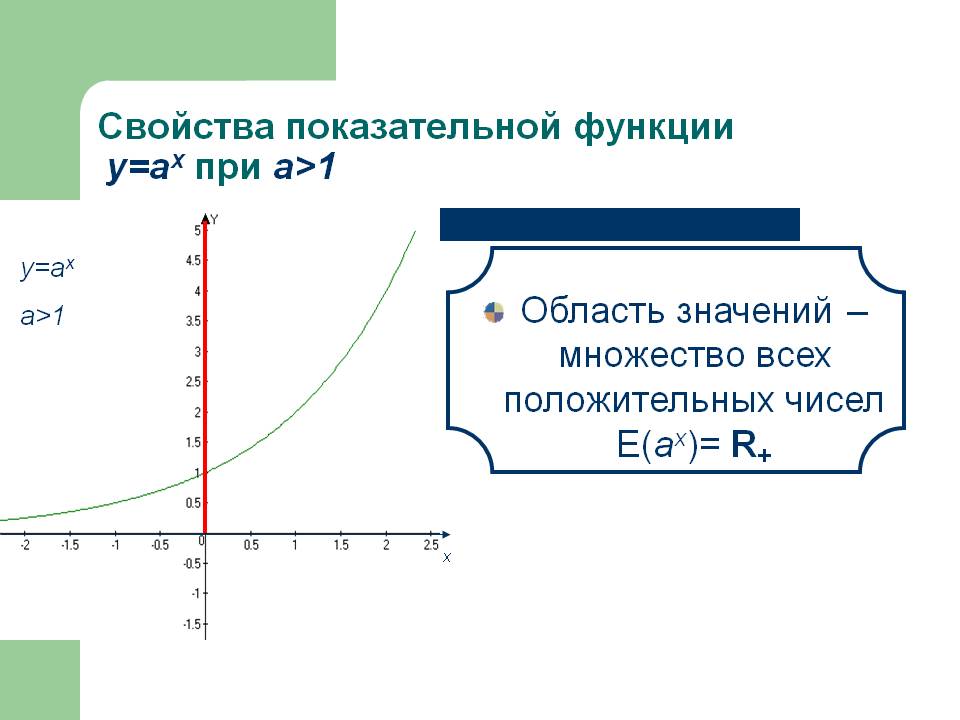
Свойства показательной функции у=аx при а>1. Область значений – множество всех положительных чисел E(аx)= R+. Х.
Скачать презентацию
Алгебра 11 класс
краткое содержание других презентаций«Тригонометрия» - Тригонометрические формулы. Получение функции arctg. Целое число. Треугольник. Формулы приведения. Тригонометрический круг. Непрерывность. Свойства функции arctg. Трегонометрические функции. Графики версинуса. Численные значения. Функции y=arcctg x. Использование. Некоторые формулы приведения. Редко используемые тригонометрические функции. Область определения. Тангенс. Функция arcsin. Тригонометрические функции комплексного аргумента.
«Основные свойства функции» - График нечетной функции симметричен относительно начала координат. График функции. Нули функции. Способы задания функций. Наибольшее и наименьшее значения. Четная функция. Промежутки знакопостоянства. Ограниченность. Четность. Свойства функции. Выпуклость. Определение функции. Непрерывность. Монотонность. Определите, на каком из рисунков изображен график непрерывной функции . Область значений. Способы задания функции.
«Решение показательных уравнений и неравенств» - Уравнение. Показательные уравнения. Ключевые понятия. Показательные неравенства. Какая из данных функций является возрастающей. Обобщение и системазация понятий. Решите уравнение. Структурные элементы урока. Показательная функция. Решите систему уравнений. Решение показательных уравнений и неравенств. Функция. Найдите область значений функции. Экстремумы. Система уравнений. Решите графически неравенство.
««Степенные функции» 11 класс» - Функция у=х4. Функция у = х2n-1. Функция у=х0. Степенные функции с натуральным показателем. У = х. Функция у = х2n. Графиком является парабола. Гипербола. Функция у=х-2. Функция у=х-3. Степенная функция. Кубическая функция.
««Логарифмические неравенства» 11 класс» - Определение. При а>1 логарифмическая функция у=lоgаx возрастает. При 0<а<1 логарифмическая функция у=lоgаx убывает. При 0<а<1, неравенство logа f(x)>logа g(x) равносильно неравенству противоположного смысла: f(x) < g(x). ?. Если а>1, то logа f(x)>logа g(x) ? Если 0<а<1, то logа f(x)>logа g(x) ?. Сравните числа: log26 … log210 log0,36 … log0,310. Повторить свойства логарифмической функции. Правильный ответ:
«Соединения в комбинаторике» - Бином Ньютона. 8 участниц финального забега. Обобщение правила произведения. Виды соединений. Полный перебор. Размещения. Встретились пятеро. Виды соединений в комбинаторике. Сочетания. Знакомство с теорией соединений. Букет. Метод решения комбинаторных задач. Перестановки. Разные стороны. Правило произведения. Возникновение комбинаторики. Лишних знаний не бывает. Основные задачи комбинаторики. Раздел математики.
Всего в теме «Алгебра 11 класс» 35 презентаций