Исследовать на экстремумы функцию у = х3 - 3x2 - 9х + 5 (5) и |
|
Скачать презентацию |
||
| << Теорема 3.(достаточные условия максимума и минимума) | Выводы >> |
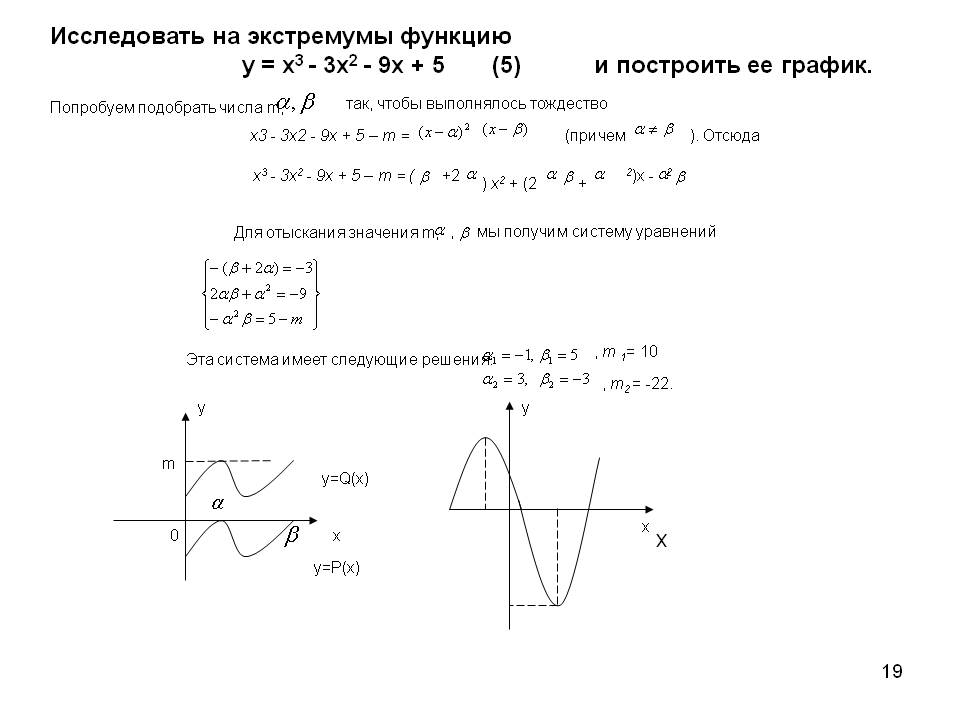
Исследовать на экстремумы функцию у = х3 - 3x2 - 9х + 5 (5) и построить ее график. Попробуем подобрать числа m, y=Q(x). Х. 19. Так, чтобы выполнялось тождество. Х3 - 3x2 - 9х + 5 – m =. (Причем. ). Отсюда. Х3 - 3x2 - 9х + 5 – m = (. +2. 2)х -. 2. ) x2 + (2. +. Для отыскания значения m, , Мы получим систему уравнений. , m 1= 10. Эта система имеет следующие решения: , m2 = -22. У. У. m. Х. 0. Х. y=P(x).
Скачать презентацию
Алгебра 11 класс
краткое содержание других презентаций«Показательные и логарифмические неравенства» - Простейшими показательными неравенствами называются неравенства вида. 2. Логарифмические неравенства 2.1. Решение простейших логарифмических неравенств. Решение: Лекция №5. 1.4. Решение сложных показательных неравенств. Государственное Образовательное Учреждение Лицей №1523 ЮАО г.Москва. 1. Показательные неравенства 1.1. Решение простейших показательных неравенств. 1.3. Решение показательных неравенств с помощью замены переменных.
«Применение определённого интеграла» - Суммы Дарбу. §3. Вычисление длины кривой. §2. Площадь трапеции, выраженная интегралом. §4. Список литературы. Определенный интеграл. §4. Гл. 4. Разработка факультатива по теме «Определенный интеграл». Интегральная сумма. §4. Объем тела вращения. §6. Гл. 2. Различные подходы теории интеграла в учебных пособиях для школьников. §1. Нахождение статических моментов и центра тяжести кривой. §7. Гл. 1. Неопределенные и определенные интегралы. §1.
«Решение логарифмических неравенств» - Решите неравенство. Логарифмические неравенства. Алгебра 11 класс.
«Правила дифференцирования» - Как называется операция нахождения производной ? Каким может быть число h в отношении ? Свойства производных? Фронтальный опрос. Вопросы: Что называется производной функции f(x) в точке x ? Урок по алгебре и началам анализа (11 класс) Правила дифференцирования. Правила дифференцирования. Тип урока: урок повторения и обобщения полученных знаний.
«Системы координат» - Выполнила: Лазарева Юлия, 11 Б класс. Полярная ?геодезическая система координат. Системы координат. Точка в цилиндрических координатах. Координаты Риндлера. Формулы перехода от декартовой системы координат к полярной: Аффинная (косоугольная) система координат. ? Полярная система координат.
«Уравнения третьей степени» - Х3 + b = ax (3). Наша формула дает: Второй пример: г.Северодвинск. Первый пример: Исследовательская работа. Решение уравнений третьей степени. Объект исследования: уравнения третьей степени. Здесь р = 6 и q = -2.
Всего в теме «Алгебра 11 класс» 35 презентаций