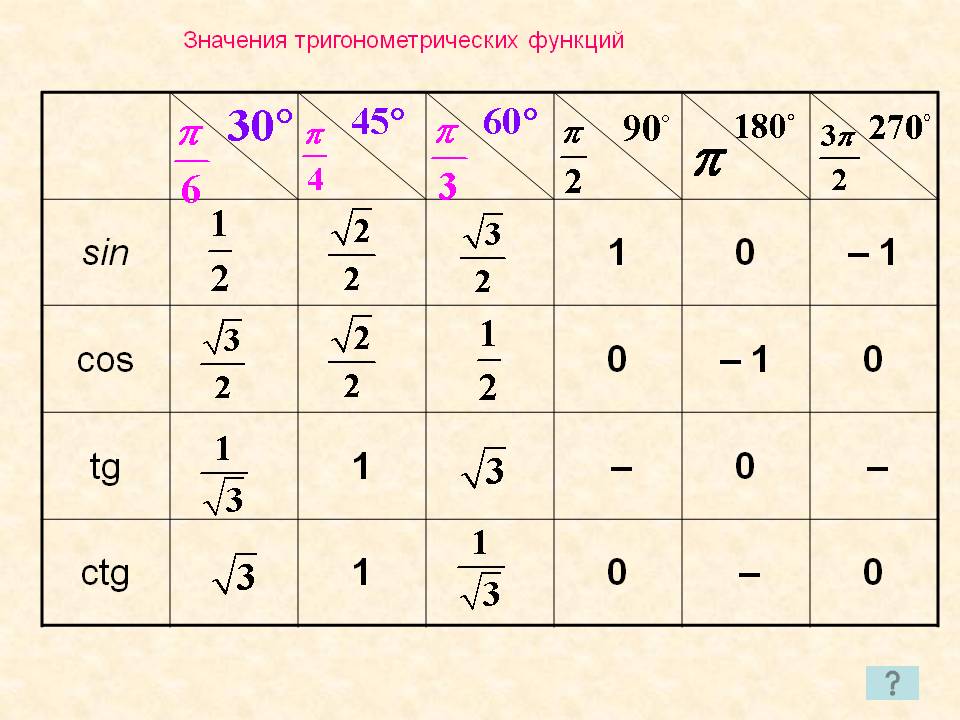
Значения тригонометрических функций

Слайд 11 из презентации «Тригонометрические функции». Размер архива с презентацией 380 КБ.

Скачать презентацию

Алгебра 9 класс

краткое содержание других презентаций

«Арифметическая прогрессия 9 класс» - Знание свойств арифметической прогрессии позволяет решать не мало различных задач. а1, а2, а3, а4, …, аn – последовательность, где аn+1 = an + d. Задать прогрессию – указать а1 и d. Или. Арифметическая прогрессия. Сумма n-первых членов арифметической прогрессии: Аn = а1 + d(n – 1) – формула n-го члена прогрессии. Искомая сумма оказывается равной. Разность прогрессии: d = an+1 – an.

«Решение квадратных уравнений 9 класс» - Задачи курса: Решим уравнение х2 + 10х - 24=0. Анкетирование. Решение кв. уравнений с помощью «номограмм» 1ч. Пояснительная записка Тематическое планирование Информационное обеспечение Приложение. Определение кв.уравнения. =. Решим уравнение х2 + 6х - 7=0 х2 + 6х - 7=х2 + 2х3 + 32 - 32 - 7=(х-3)2 - 9- 7= (х-3)2 - 16 (х-3)2 -16=0 (х-3)2 =16 х-3=4 или х-3=-4 х=1 х=-7 Ответ: х1=1, х2 =-7. Метод выделения полного квадрата.

«Задачи по арифметической прогрессии» - Содержание: Верно. Арифметическая прогрессия 9 класс. Рефлексия. Формулы арифметической прогрессии: В содержание. В какой фигуре записана арифметическая прогрессия? Найдите первые четыре члена арифметической прогрессии, заданной формулой: Не верно. Сегодня на уроке я хочу …

«Геометрическая прогрессия» - Решение задачи: b1 = 1, q =2, n =30. Диаметры кругов образуют бесконечно убывающую геометрическую прогрессию. Bn = b1· qn – 1 – формула n-го члена прогрессии. Бесконечная сумма оказалась равна вполне конечной величине – высоте треугольника. Сумма n-первых членов геометрической прогрессии: В пространство над вторым – третий. Купец обрадовался такой удаче. Сумма бесконечной убывающей геометрической прогрессии:

«Последовательность» - Последовательности могут быть конечными и бесконечными, возрастающими и убывающими. «Последовательности». 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1. Историческая справка. Последовательности составляют такие элементы природы, которые можно как то пронумеровать. Между числами Фибоначчи и треугольником Паскаля существует интересная связь.

«Тригонометрические функции» - С точностью до знака в зависимости от четверти, в которой расположена точка. У. –. 1. 3. Свойства синуса, косинуса, тангенса и котангенса. Если M (t) = M (x; y), то. •. – 1. Числовая окружность. А. +.

Всего в теме «Алгебра 9 класс» 48 презентаций